How Huffman's algorithm works
Huffman coding
Huffman coding is a data compression algorithm used to reduce data size and generate optimal, variable-length coding.
In fixed-length encoding, all the letters/symbols are represented using an equal number of bits.
For example:
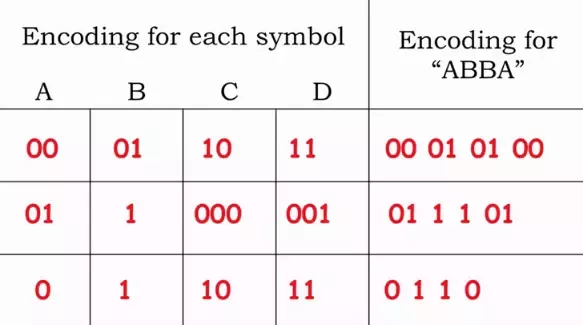
Here, the first row is fixed-length encoding where all the symbols are represented using an equal number of bits. Fixed length encodings have the advantage of random access. Since every letter contains an equal number of bits, if we wanted to, for example, see what the 4th letter is, we would skip the appropriate amount of bits. Fixed length encodings work well when all the possible choices have an equal probability of occurring.
In languages (e.g., English), some letters occur more frequently than others. Therefore, it would be very inefficient to use lengthier bit representations for letters that occur very frequently.
However, we face certain problems when we try to represent a frequently occurring “e” with a 0, and a rare “z” with a 110.
When we try to decode the third row from the table, which is " 0 1 1 0", it could mean :
- “ABBA” = 0 1 1 0
- “ADA” = 0 11 0
- “ABC” = 0 1 10
This kind of encoding is wrong since it is ambiguous.
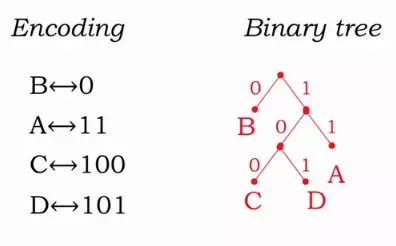
To avoid such ambiguity we need a binary tree representation.
The above image shows how to encode with a binary tree. Every time we finish decoding a letter, we start at the root again.
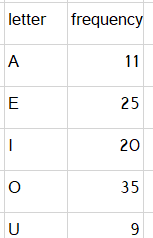
Suppose we are asked to decode “1100101”, we would start at the root and traverse the binary tree until a leaf was found. This encoding gives us the answer “ABBD”. Now, suppose you are given certain symbols and the frequency in which they occur:
Huffman coding gives us a method to build a binary tree for the letters in the table above.
The Huffman Algorithm has a “bottom-up” approach, meaning we start with the tree’s leaf nodes. The algorithm states that we should start with the symbols that have the lowest frequency. So, we start with the letter with the lowest frequency, which is, in this case, U(9) and A(11).
- Since we added two leaf nodes to the bottom, their root will add the two frequencies together to get 20. The next is “I”:
Then E and O. So the final tree will look like:
Note: while traversing the left child of a node, we will append
0and1for the right child.
The left branch is arbitrarily chosen to be 0 and the right is chosen 1.
So, if we wanted to encode AEIOU it would be, 001110110000
Explaination
Say your country is at war and can be attacked by two enemies(or both at the same time), and you are in charge of sending out messages every hour to your country’s military head if you spot an enemy aircraft.
However, instead of sending long messages, you decide to send codes instead, like the following: 00 - No aircraft spotted 01 - Enemy 1 aircraft spotted 10 - Enemy 2 aircraft spotted 11 - Both Enemy 1 aircraft and Enemy 2 aircraft spotted
But your military head is a busy man and will see multiple messages at one time. For example, he reads 000000000000000110(length 20). Since each code is of two symbols he is able to decode it quite easily. For 8 consecutive hours, no enemy aircraft is spotted and then Enemy 1 is spotted and then enemy 2.
You soon realize that you are, most of the time, just sending out a bunch of zeros, and that the code could be made much shorter if you used a shorter code for no aircraft being spotted, i.e., the more probable event. Once you begin to use a shorter code for the more probable event, you will be able to send shorter messages.
0 - No aircraft spotted 1 - Enemy 1 aircraft spotted 01 - Enemy 2 aircraft spotted 10 - Both Enemy 1 aircraft and Enemy 2 aircraft spotted
Brilliant job! You have shortened the codes you need to send. So, you go ahead and send 00000000101(length 11). Your military head goes crazy on seeing this. He is not able to decode it properly. This might mean you didn’t see anything for 8 hours and then enemy 1 and then enemy 2, but it also might mean you didn’t see anything for 7 hours then spotted enemy 2’s aircraft twice. So, your code does not decode to a unique situation.
Huffman codes ensure that no code is the prefix of another code (such as how 0 was the prefix of the 01 in the previous case). This ensures that the code can be decoded uniquely.
- 0 - No aircraft spotted
- 10 - Enemy 1 aircraft spotted
- 110 - Enemy 2 aircraft spotted
- 111 - Both Enemy 1 aircraft and Enemy 2 aircraft spotted
Now, your message becomes 0000000010110(length 13). Although this is a bit longer, your commander is able to decode it perfectly.
So, Huffman’s algorithm is good for two things:
- Shorter codes for more probable events so that the messages you send are short on average.
- Prefix-free codes so that the messages you send are uniquely decodable.