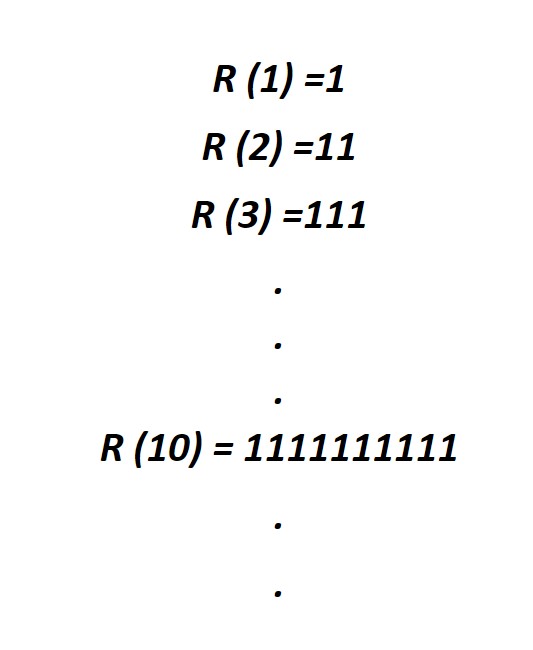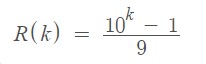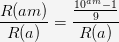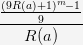Project Euler: What are repunit nonfactors?

Repunits

Repunits are defined as numbers that consist of all ones. For example: 1111111,1111, …

Repunit is denoted by R(k), where k is the number’s length (number of digits). The examples are shown below:

Repunit nonfactors problem

For this problem, let’s consider a repunit that can be represented in the form of $R(10^n)$.

We can see that for n = 1 , 2 and 3, $R(10)$, $R(100)$, and $R(1000)$ are not divisible by 17, but there is still a value, n=4, for which $R(10000)$ is divisible by 17.

However, there is no value for n for which $R(10^n)$ is divisible by 19. In fact, we can conclude that below one-hundred, only the following four prime numbers are factors of $R(10^n)$: 11, 17, 41, and 73.

We know that repunit can also be written as follows:

Let k = am, where k , a , and m are all positive integers, and then we divide $R(am)$ by $R(a)$. We then have:

From the definition of repunit $R(k) = (10^k - 1)/9$ , we can conclude that $10^k = 9*R(k) +1$ .

Then,
$10^a = 9*10(a)+1$ and $10^am = ( 9*10(a)+1)^m$.

If we insert the discussions above in the previous formulas, we get:

If we observe the previous formula, the upper term above yields the expression that will contain + 1 in the end (exponent expansion), and this +1 will be canceled by -1 in the numerator. Now, in the numerator, we only have an expression in which each term will have 9 or its multiples. So, this shows that the whole term is divisible by 9.

We need to find the sum of all prime numbers below one-hundred thousand that will never be the factor of $R(10^n)$.

Code

The solution for this problem can be found with the following code. We use prime_seive from the Euler library.

The correct solution for this problem was found in 0.02 seconds on Intel core i7-2600K CPU @ 3.4 GHz (compiled in x86-64/Linux).