What is a z-score and its significance in a dataset?
The z-score is a concept widely used in probability and statistics. It is used when data is normally distributed. To understand z-score better, we first need to know what a normal distribution is.
Normal distribution
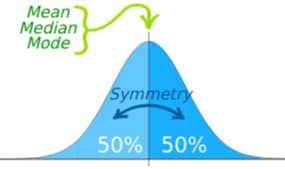
The figure below shows a normal distribution curve:
In normally distributed data, data lying above and below the mean is proportionate. The resulting curve is of a bell shape. The center of the curve denotes the mean.
The mean, mode, and median are all equal.
The area under the curve is 1. The curve is symmetrical about the mean.
Background
Oftentimes, we need to compare values from different datasets. Let’s suppose a university accepts ACT and SAT scores for admissions. Both these tests have different metrics, cumulative scores, and hence different means. How can the university compare results from each test and decide which student performed better than the other? In such situations, we need to standardize the scores to compare them. The resulting standardized normal variable for each score is called Z.
A random normal variable
Xis standardized to have a mean of 0 and a standard deviation of 1.
z-scoreis used when the data is normally distributed.
The
z-scorewill tell us how many standard deviations above or below the mean does a value lie.
Mathematical formulation
Let’s familiarize with some terminology before we craft a formula:
| Symbol | Name | Purpose |
|---|---|---|
| z | Standard Normal Variable | Standardized score |
| Random Normal Variable | Actual value | |
| mu | Mean of the data | |
| sigma | Standard deviation of the data |
To standardize a random normal variable, we need to carry out the following steps:
- Subtract the mean () from the random normal variable ().
- Divide the result by the standard deviation ()
The final formula is as follows:
z=
The illustration below summarizes the procedure:
Calculating mean
Mean is the average of all values in the data. It is calculated as follows:
- Take the sum of all values in the dataset.
- Divide by the total number of values.
The final formula is as follows:
=
where is each Random Normal Variable and is the number of values.
Calculating standard deviation
Standard deviation indicates how far a value is from the mean. It is calculated as follows:
- Subtract the mean from each value of .
- Take the square of the result of each of the value above.
- Add all these squares together.
- Divide by the number of values in the dataset.
- Take the square of the result of the previous step.
The final formula is as follows:
=
Example
We have gathered all the bits of information we need to work with z-score. Let’s work through a simple example:
Suppose 15 students in a class took a test. The professor wants to ensure that he grades them realistically. Therefore, he decides that whoever scores more than 1 standard deviation below the mean will fail while others will pass. The table below shows the summary of scores:
| Student | Test Scores (out of 100) |
|---|---|
| Jack | 72 |
| Jim | 86 |
| Gabe | 56 |
| Bill | 92 |
| Alice | 78 |
| Veronica | 94 |
| Angelica | 32 |
| Matt | 44 |
| Thomas | 66 |
| Dice | 100 |
| Donald | 28 |
| Rice | 42 |
| Jones | 88 |
| Chris | 79 |
| Liam | 73 |
In order to discuss these scores in terms of standard deviation, we need to standardize them. To do so, we will calculate the z-score for each.
Remember! Standardized scores have a mean of 0 and standard deviation of 1.
Finding mean
Total number of values are 15. Therefore, .
Step 1: Taking sum
Sum
Step 2: Divide by
The mean is 68.7.
Finding Standard deviation
Follow the steps discussed above to calculate the standard deviation.
It will look something like this:
= =
The standard deviation is 22.4.
Finding z-score
We can now plug these values in the formula for z-score.
z =
For Jack:
z =
In simpler words, Jack is 0.147 standard deviations above the mean.
We can repeat the process for all the students. The updated table below shows the z-score of each student as well:
| Student | Test Scores (out of 100) | z-score |
|---|---|---|
| Jack | 72 | 0.147 |
| Jim | 86 | 0.772 |
| Gabe | 56 | -0.567 |
| Bill | 92 | 1.04 |
| Alice | 78 | 0.415 |
| Veronica | 94 | 1.129 |
| Angelica | 32 | -1.638 |
| Matt | 44 | -1.102 |
| Thomas | 66 | -0.120 |
| Dice | 100 | 1.400 |
| Donald | 28 | -1.817 |
| Rice | 42 | -1.192 |
| Jones | 88 | 0.861 |
| Chris | 79 | 0.460 |
| Liam | 73 | 0.192 |
Results
As the table above shows, Angelica, Matt, Donald, and Rice score more than 1 standard deviation below the mean. Hence, they failed the test.
Other areas of usage
The z-score follows the same pattern of calculation in statistical inference as well. In statistical inference, we need to validate whether a hypothesis generalizes to the entire population or is only applicable to the sample data. For such purposes, statisticians carry out hypothesis testing which requires standardizing data and calculating z-scores.
Similarly, when comparing two datasets with different metrics of calculations, we can use the z-score as a standardized metric.
Free Resources