What is the 0-1 knapsack problem?

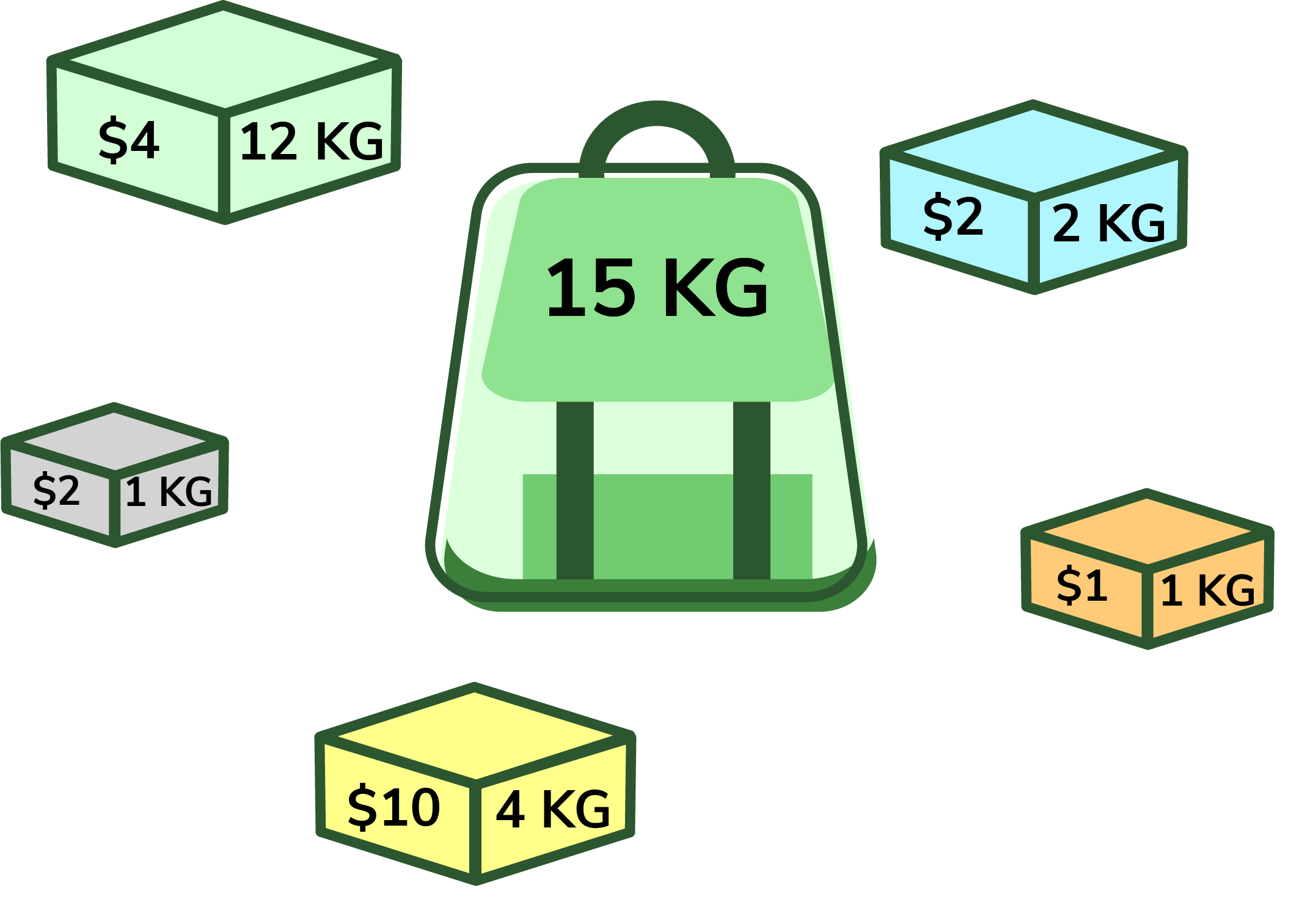
The 0-1 knapsack problem refers to a situation in which, during the filling of a knapsack, items are either taken in their entirety or not taken at all. For instance, consider two items weighing 3kg and 5kg, respectively. If we choose the 5kg item, we cannot select just 1kg from it (as the item cannot be divided) — we must take the whole 5kg item.

Home/Blog/Programming/Demystifying the 0-1 knapsack problem: top solutions explained

Demystifying the 0-1 knapsack problem: top solutions explained

Ryan Thelin

Nov 20, 2023

7 min read

content

What is the knapsack problem?Knapsack Question Variants What skills does it test?Brute-force recursive solution Solution Explanation Optimized dynamic programming solution Solution Explanation What to learn next Continue reading about coding interview questions

Become a Software Engineer in Months, Not Years

From your first line of code, to your first day on the job — Educative has you covered. Join 2M+ developers learning in-demand programming skills.

In any dynamic programming coding interview you take, you’ll likely encounter the knapsack problem. This question is often a source of anxiety to interviewees because of the complexity of the solution and the number of variants of the problem.

Today, we’ll get you comfortable with the knapsack problem in multiple languages by exploring two popular solutions, the recursive solution and top-down dynamic programming algorithm solution. By the end of the article, you’ll have the experience needed to solve the knapsack problem with confidence.

What is the knapsack problem?#

The knapsack problem is one of the top dynamic programming interview questions for computer science.

The problem statement is:

You’re a burglar with a knapsack that can hold a total weight of capacity. You have a set of items (n items) each with fixed weight capacities and values. The weight and value are represented in an integer array. Create a function knapsack() that finds a subset or number of these items that will maximize value but whose total weight does not exceed the given number capacity.

Knapsack Question Variants#

There are two major variants of this question, fractional or 0-1. The fractional variant allows you to break items to maximize the value in the pack. The 0-1 variant does not allow you to break items.

Another common variant is the constrained knapsack problem that restricts your program so you cannot select any item more than once. When an element is selected, the program must decide if it should place it in the pack or leave it.

At senior level interviews, you’ll encounter variants that add volume as a constrained attribute. In this case, each item also has a fixed volume, and the knapsack has a volume limit.

What skills does it test?#

This problem is so popular because it tests many desired skills at once and can be altered to throw interviewees off balance. In other words, you have to really understand the logic of the problem and code. Simple memorization won’t take you far.

The optimal solution for the knapsack problem is always a dynamic programming solution. The interviewer can use this question to test your dynamic programming skills and see if you work for an optimized solution.

Another popular solution to the knapsack problem uses recursion. Interviewers may ask you to produce both a recursive and dynamic solution if they value both skill sets. This is a popular choice because interviewers can see how well you shift from a recursive to a dynamic solution.

The knapsack problem also tests how well you approach combinatorial optimization problems. This has many practical applications in the workplace, as all combinatorial optimization problems seek maximum benefit within constraints.

For example, combinatorial optimization is used in solutions like:

Determine the best programs to run on a limited resource cloud system
Optimize water distribution across a fixed pipe network
Automatically plan the best package delivery route
Optimize the company’s supply chain

You can expect this question to be asked for any role that manages or creates automated optimization software.

Brute-force recursive solution#

The most obvious solution to this problem is brute force recursive. This solution is brute-force because it evaluates the total weight and value of all possible subsets, then selects the subset with the highest value that is still under the weight limit.

While this is an effective solution, it is not optimal because the time complexity is exponential. Use this solution if you’re asked for a recursive approach. It can also be a good starting point for the dynamic solution.

Time complexity: $O(2^{n})$ , due to the number of calls with overlapping subcalls

Auxiliary space: $O(1)$ , no additional storage is needed.

#include <iostream>
using namespace std;
// Returns the maximum value that can be put in a knapsack of capacity W 
int knapsackRecursive(int profits[], int profitsLength, int weights[], int capacity, int currentIndex) {
  // Base Case 
  if (capacity <= 0 || currentIndex >= profitsLength || currentIndex < 0)
    return 0;
  // If weight of the nth item is more than Knapsack capacity W, then 
  // this item cannot be included in the optimal solution
  int profit1 = 0;
  if (weights[currentIndex] <= capacity)
    profit1 = profits[currentIndex] + knapsackRecursive(profits, profitsLength, weights, capacity - weights[currentIndex], currentIndex + 1);
  int profit2 = knapsackRecursive(profits, profitsLength, weights, capacity, currentIndex + 1);
  // Return the maximum of two cases:  
  // (1) nth item included  
  // (2) not included 
  return max(profit1, profit2);
}
int knapSack(int profits[], int profitsLength, int weights[], int capacity) {
  return knapsackRecursive(profits, profitsLength, weights, capacity, 0);
}
int main() {
  int profits[] = {1, 6, 10, 16}; // The values of the jewelry
  int weights[] = {1, 2, 3, 5}; // The weight of each
  cout << "Total knapsack profit = " << knapSack(profits, 4, weights, 7) << endl;
  cout << "Total knapsack profit = " << knapSack(profits, 4, weights, 6) << endl;
}

Explanation#

Line numbers within explanation refer to the C++ version from above

On line 14, we start from the beginning of the weight array and check if the item is within the maximum capacity. If it is, we call the knapsack() function recursively with the item and save the result in profit1.

Then we recursively call the function, exclude the item, and save the result in the profit2 variable. On line 21, we return the greater of profit1 and profit2

Pseudocode:

Here’s a pseudocode explanation of how this program functions.

for each item 'i' starting from the end
  create a new set which INCLUDES item 'i' if the total weight does not exceed the capacity, and recursively process the remaining capacity and items
  create a new set WITHOUT item 'i', and recursively process the remaining items 
 
return the set from the above two sets with higher profit

This program contains many overlapping subproblems, but they’re calculated each time rather than stored. Repeated calculations increase runtime drastically. To avoid recalculating we can instead use dynamic programming to memoize the solution to subproblems for reuse.

Optimized dynamic programming solution#

Now, we’ll optimize our recursive solution through the addition of top-down dynamic programming to handle the overlapping subproblems.

Since we have two changing values (capacity and currentIndex) in our recursive function knapsackRecursive(), we can use a two-dimensional array to store the results of all the solved sub-problems. As mentioned above, we need to store results for every sub-array (i.e. for every possible index i) and for every possible capacity c.

This is the optimal solution for the knapsack problem in both time and space complexity.

Time complexity: $O(N*C)$ , our memoization table stores results for all subproblems and will have a maximum of $N*C$ subproblems.

Auxiliary space: $O(N*C + N)$ , $O(N*C)$ space for the memoization table, and $O(N)$ space for recursion call-stack.

Tips: During the interview, make sure to talk through your thought process with the interviewer so they can see your problem-solving skills.

#include <iostream>
#include <vector>
using namespace std;
int knapsackRecursive(vector< vector<int> > lookupTable, int profits[], int profitsLength, int weights[], int capacity, int currentIndex) {
  // base checks  
  if (capacity <= 0 || currentIndex >= profitsLength || currentIndex < 0)
    return 0;
  // if we have already solved the problem, return the result from the table  
  if (lookupTable[currentIndex][capacity] != 0)
    return lookupTable[currentIndex][capacity];
  // recursive call after choosing the element at the currentIndex
  // if the weight of the element at currentIndex exceeds the capacity, we shouldn't process this
  int profit1 = 0;
  if (weights[currentIndex] <= capacity)
    profit1 = profits[currentIndex] + knapsackRecursive(lookupTable, profits, profitsLength, weights,
      capacity - weights[currentIndex], currentIndex + 1);
  // recursive call after excluding the element at the currentIndex
  int profit2 = knapsackRecursive(lookupTable, profits, profitsLength, weights, capacity, currentIndex + 1);
  lookupTable[currentIndex][capacity] = max(profit1, profit2);
  return lookupTable[currentIndex][capacity];
}
int knapSack(int profits[], int profitsLength, int weights[], int capacity) {
  vector< vector<int> > lookupTable(
    profitsLength,
    std::vector<int>(capacity + 1, 0));
  return knapsackRecursive(lookupTable, profits, profitsLength, weights, capacity, 0);
}
int main() {
    int profits[] = {1, 6, 10, 16};
    int weights[] = {1, 2, 3, 5};
    cout << "Total knapsack profit = " << knapSack(profits,4, weights, 7) << endl;
    cout << "Total knapsack profit = " << knapSack(profits,4, weights, 6) << endl;
}

Explanation#

To implement dynamic programming we only need to change 5 lines.

In line 9, we create a two-dimensional array, dp, to hold the results of any solved subproblem. This allows us to use these memoized solutions later rather than recalculating the answer.

In lines 22 and 23, we create a case that checks dp to see if the current sub-problem’s solution has already been found. If we have, we return the memoized solution and move onto the next subproblem.

In lines 38, we calculate the maximum possible value of the bag if we include the current item in profit1 and the maximum value of the bag if we exclude the current item in profit2. We then save the higher of these in our two-dimensional array dp.

In line 39, we return the item that makes the highest knapsack value. This is a partial result that ends one recursive call before the next begins. Once this has occurred for all possible combinations, the first call will return the actual result.

What to learn next#

Thanks for completing this deep dive into the 0-1 knapsack problem. Confidence with dynamic programming coding interview questions comes from practice and exposure to popular problem different variants.

As you’re preparing for your next coding interview, here are some more DP questions you’ll want to study:

Longest common substring problem
Palindrome subsequence problem
Fibonacci numbers problem
Staircase problem
Coin change problem

Educative’s course, Grokking Dynamic Programming Patterns for Coding Interviews, contains solutions to all these problems in multiple programming languages. Each solution has an in-depth, line-by-line solution breakdown to ensure you can expertly explain each solution to the interviewer. By the end of the course, you’ll be able to walk into dynamic programming coding interviews confident that you’re prepared for anything they can throw at you.

Happy interviewing!

Continue reading about coding interview questions#

Free Resources

Learn in-demand tech skills in half the time

PRODUCTS

Mock Interview

New

Courses

Skill Paths

Projects

Assessments

Demystifying the 0-1 knapsack problem: top solutions explained

What is the knapsack problem?#

Knapsack Question Variants#

What skills does it test?#

Brute-force recursive solution#

Solution#

Explanation#

Optimized dynamic programming solution#

Solution#

Explanation#

What to learn next#

Continue reading about coding interview questions#

Frequently Asked Questions

What is the 0-1 knapsack problem?