Algorithms 101: How to use graph algorithms

Algorithms are one of the most common themes in coding interviews. In order to gain an advantage in interviews, it is important to be very familiar with the top algorithms and their implementations.

In today’s tutorial, we will be exploring graph algorithms. We’ll begin with an introduction to graph theory and graph algorithms. Next, we will learn how to implement a graph. Finally, we will examine common graph problems you can expect to see in a coding interview.

Prepare for algorithm questions the easy way

This curates path takes you through all that you need to know to crack your Python interviews with confidence.

Ace the Python Coding Interview

What are graph algorithms?#

An algorithm is a mathematical process to solve a problem using a well-defined or optimal number of steps. It is simply the basic technique used to get a specific job done.

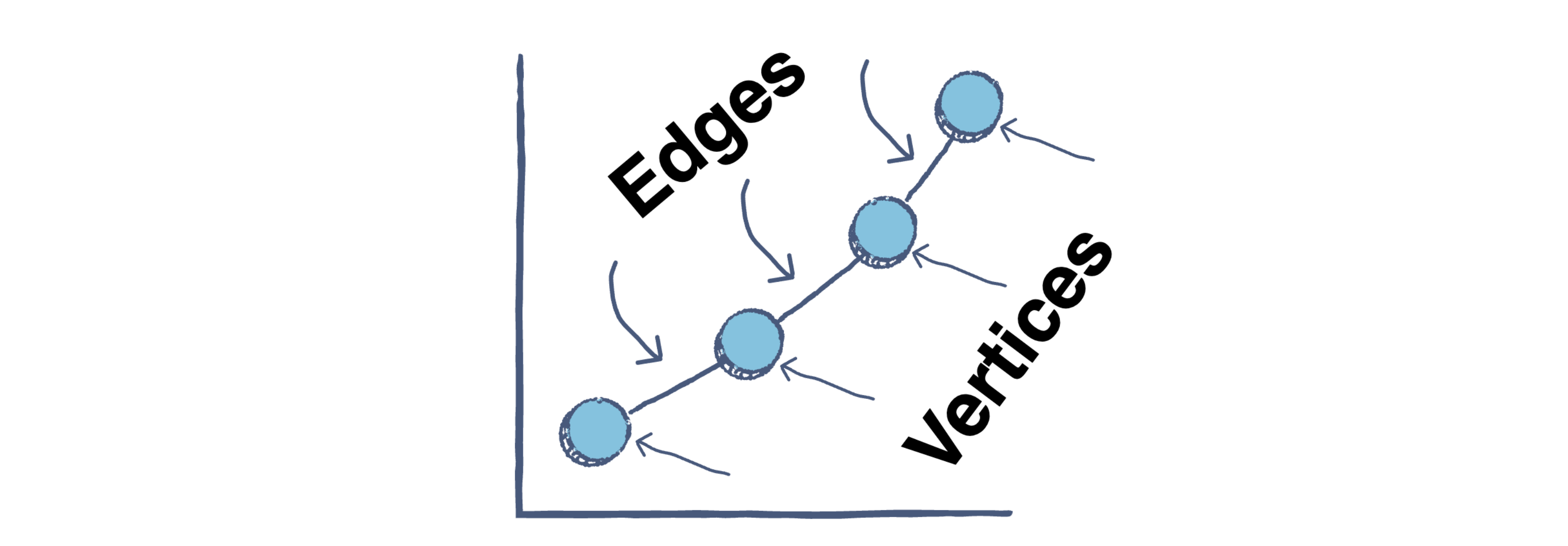
A graph is an abstract notation used to represent the connection between all pairs of objects. Graphs are widely-used mathematical structures visualized by two basic components: nodes and edges.

Graph algorithms are used to solve the problems of representing graphs as networks like airline flights, how the Internet is connected, or social network connectivity on Facebook. They are also popular in NLP and machine learning to form networks.

Some of the top graph algorithms include:

• Implement breadth-first traversal
• Implement depth-first traversal
• Calculate the number of nodes in a graph level
• Find all paths between two nodes
• Find all connected components of a graph
• Dijkstra’s algorithm to find shortest path in graph data
• Remove an edge

While graphs form an integral part of discrete mathematics, they also have practical uses in computer science and programming, including the following:

• Caller-callee relationships in a computer program represented as a graph
• The link structure of a website could be represented by a directed graph
• Neural networks

Properties of a graph#

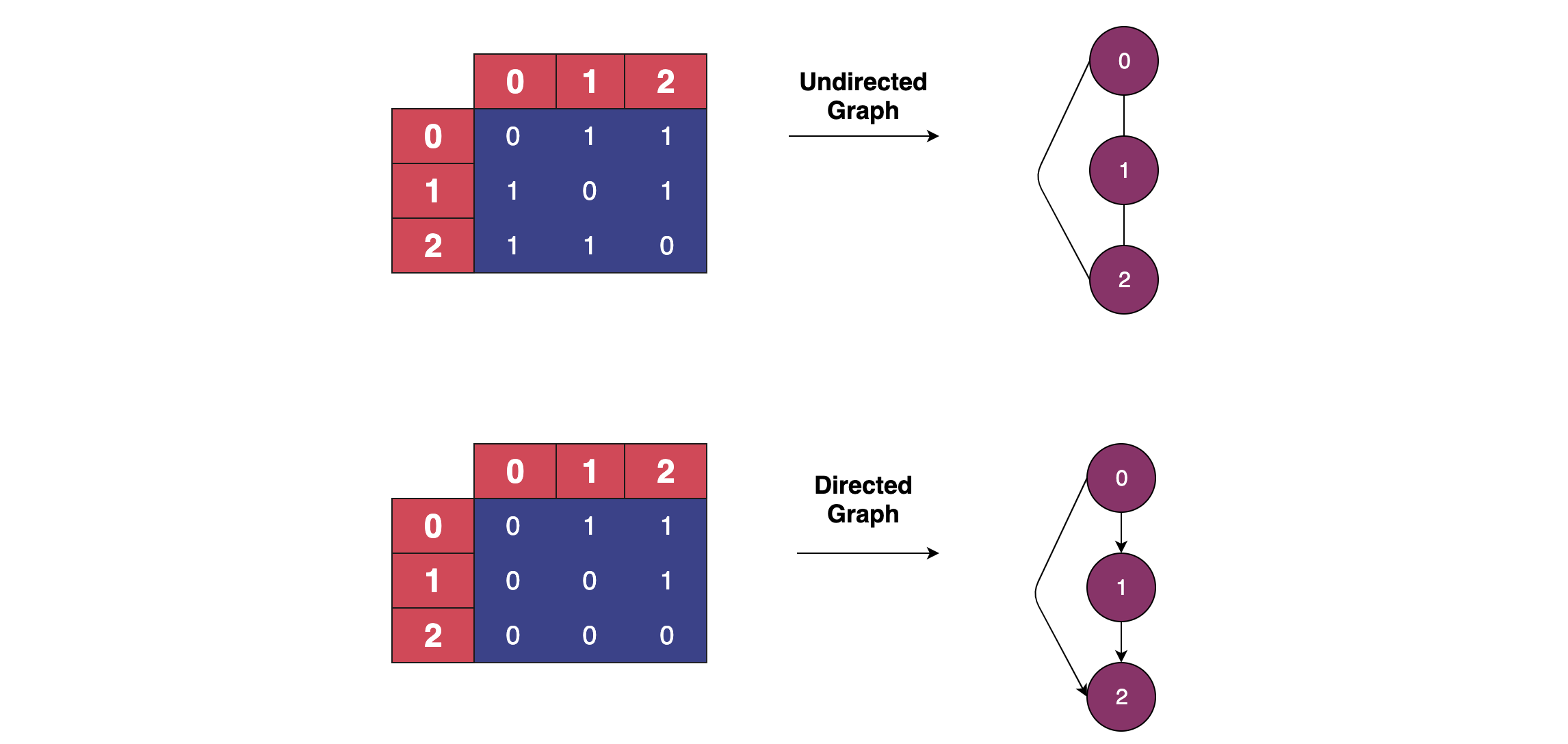
A graph, denoted by G, is represented by a set of vertices (V) or nodes linked at edges (E). The number of edges you have depends on the vertices. The edges may be directed or undirected.

In a directed graph, the nodes are linked in one direction. The edges here show a one-way relationship.

In an undirected graph, the edges are bi-directional, showing a two-way relationship.

Example: A good use-case of an undirected graph is Facebook friend suggestions algorithm. The user (node) has an edge running to a friend A (another node) who is in turn connected (or has an edge running) to friend B. Friend B is then suggested to the user.

There are many other complex types of graphs that fall into different subsets. A directed graphs, for example, has strongly connected components when every vertex is reachable from every other vertex.

Vertex#

A vertex is a point where multiple lines meet. It is also called a node.

Edge#

An edge is a mathematical term used for a line that connects two vertices. Many edges can be formed from a single vertex. However, without a vertex, an edge cannot be formed. T​here must be a starting and ending vertex for each edge.

Path#

A path in a graph $G = (V,E)$ is a sequence of vertices v1, v2, …, vk, with the property that there are edges between $vi$ and $vi+1$. We say that the path goes from $v1$ to $vk$.

The sequence 6,4,5,1,26,4,5,1,2 defines a path from node 6 to node 2.

Similarly, other paths can be created by traversing the edges of the graph. A path is simple, if its vertices are all different.

Walk#

Walks are paths, but they don’t require a sequence of distinct vertices.

Connected graph#

A graph is connected if for every pair of vertices $u$ and $v$, there is a path from $u$ to $v$.

Cycle#

A cycle is a path v1, v2, …, vk for which the following are true:

• $k>2k>2$
• The first $k−1$ vertices are all different
• $v1=vk$

Tree#

A tree is a connected graph that does not contain a cycle.

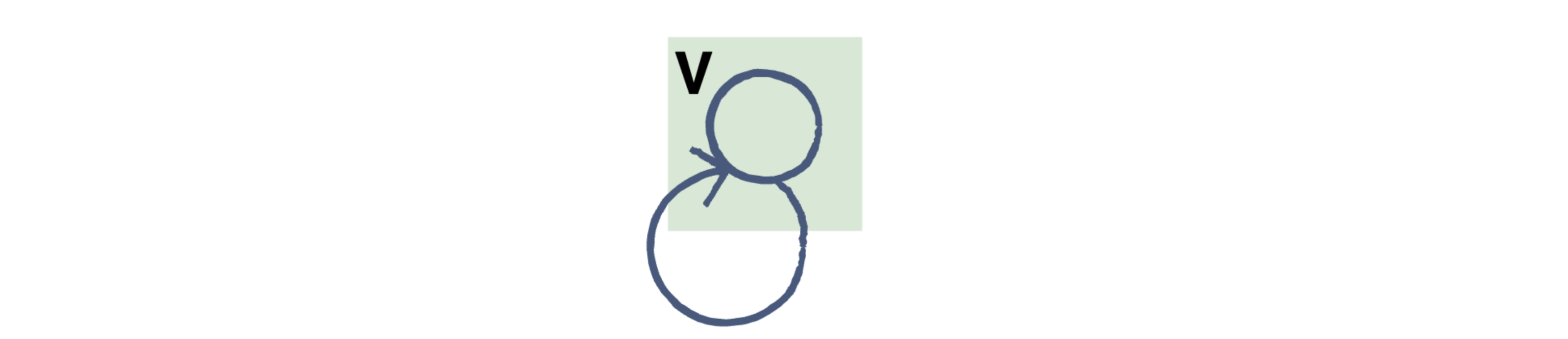
Loop#

In a graph, if an edge is drawn from the vertex to itself, it is called a loop. In the illustration, V is a vertex whose edge, (V, V), is forming a loop.

How to represent graphs in code#

Before we move on to solving problems using graph algorithms, it is important to first know how to represent graphs in code. Graphs can be represented as an adjacency matrix or adjacency list.

Adjacency Matrix#

An adjacency matrix is a square matrix labeled by graph vertices and is used to represent a finite graph. The entries of the matrix indicate whether the vertex pair is adjacent or not in the graph.

In the adjacency matrix representation, you will need to iterate through all the nodes to identify a node’s neighbors.

  a b c d e
a 1 1 - - -
b - - 1 - -
c - - - 1 -
d - 1 1 - -

Adjacency List#

An adjacency list is used to represent a finite graph. The adjacency list representation allows you to iterate through the neighbors of a node easily. Each index in the list represents the vertex, and each node that is linked with that index represents its neighboring vertices.

1 a -> { a b }
2 b -> { c }
3 c -> { d }
4 d -> { b c }

For the base graph class below, we will be using the Adjacency List implementation as it performs faster for the algorithm solutions later in this article.

The Graph Class#

The requirements of our graph implementation are fairly straightforward. We would need two data members: the total number of vertices in the graph and a list to store adjacent vertices. We also need a method to add edges or a set of edges.

In the above example, we see the Python graph class. We’ve laid down the foundation of our graph class. The variable V contains an integer specifying the total number of vertices.

Representing weighted graphs and edge weights#

Thus far, your graph representation handles only unweighted graphs.
But many real-world problems use weighted graphs, where each edge carries a cost, distance, or capacity.
You can extend your adjacency list representation to store weights (often as pairs or tuples).

Example in Python#

class Graph:
    def __init__(self, num_vertices):
        self.V = num_vertices
        self.adj = {i: [] for i in range(self.V)}

    def add_edge(self, u, v, w=1, directed=False):
        self.adj[u].append((v, w))
        if not directed:
            self.adj[v].append((u, w))

With that structure, when you traverse or compute shortest paths, you consider both the neighbor vertex and the weight.

Using weighted graphs unlocks algorithms like Dijkstra, Bellman–Ford, and Floyd–Warshall (for all-pairs), which we’ll cover next.

How to implement breadth-first traversal#

Given a graph represented as an adjacency list and a starting vertex, your code should output a string containing the vertices of the graph listed in the correct order of traversal. As you traverse the graph from the starting vertex, you are to print each node’s right child first, then the left.

To solve this problem, the previously implemented Graph class is already prepended.

Input: A graph represented as an adjacency list and a starting vertex

Output: A string containing the vertices of the graph listed in the correct order of traversal

Sample Output:

result = "02143" 
or
result = "01234"

Take a look and design a step-by-step algorithm before jumping on to the implementation. Try to solve it on your own first. If you get stuck, you can always refer to the solution provided in the solution section.

Solution#

We begin from a selected node and traverse the graph by layers. All neighbor nodes are explored. Then, we traverse we the next level. We traverse the graph horizontally, aka by each layer.

A graph may contain cycles. To avoid processing the same node again, we can use a boolean array that marks visited arrays. You can use a queue to store the node and mark it as visited. The queue should follow the First In First Out (FIFO) queuing method.

How to implement depth-first traversal#

In this problem, you have to implement the depth-first traversal. To solve this problem, the previously implemented graph class is already provided.

Input: A graph represented as an adjacency list and a starting vertex

Output: A string containing the vertices of the graph listed in the correct order of traversal

Sample Output:

result = "01342" 
or
result = "02143"

Take a look and design a step-by-step algorithm before jumping on to the implementation. Try to solve it on your own first. If you get stuck, you can always refer to the solution provided in the solution section.

Solution#

The depth-first graph algorithm uses the idea of backtracking. Here, ‘backtrack’ means to move forward as long as there are no more nodes in the current path, then to move backward on the same path to find nodes to traverse.

Shortest path algorithms: Dijkstra, Bellman–Ford, and Floyd–Warshall#

A fundamental graph problem is computing the shortest path from one node to another in a weighted graph.
Here are three core algorithms:

Dijkstra’s algorithm#

• Works with non-negative edge weights.
• Maintains a priority queue of vertices keyed by current distance.
• Iteratively “relaxes” edges to update shortest known distances.
• Complexity: O((V + E) log V) (using adjacency lists + min-heap).
• Returns shortest paths from a single source to all reachable nodes.

Bellman–Ford algorithm#

• Handles negative weights (but not negative cycles).
• Iterates up to V−1 times, relaxing all edges every iteration.
• Can detect negative cycles with one additional pass.
• Complexity: O(V * E).
• Useful when the graph may contain negative edge weights.

Floyd–Warshall algorithm#

• A dynamic programming approach for all-pairs shortest paths.
• Runs in O(V³).
• Fills a matrix dist where dist[i][j] = shortest distance from i to j.
• Can detect negative cycles if dist[i][i] becomes negative.

Example implementation#

def floyd_warshall(dist):
    n = len(dist)
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]

These algorithms expand your toolkit beyond mere traversal and open doors to solving routing, network, and path optimization problems.

Minimum spanning tree: Kruskal’s and Prim’s algorithms#

Another class of graph algorithms aims to connect all nodes with minimal total edge weight (without cycles) — namely the minimum spanning tree (MST).

Kruskal’s algorithm#

• Sorts edges by weight ascending.
• Uses a Union–Find (disjoint-set) structure to test if adding an edge would form a cycle.
• Keeps adding lowest-weight edges that don’t create cycles until all vertices are connected.
• Complexity: O(E log E) or O(E log V).

Prim’s algorithm#

• Builds the MST starting from an arbitrary vertex.
• Maintains a priority queue of edges connecting the growing tree to outside vertices.
• At each step, picks the smallest edge that adds a new vertex.
• Complexity: O(E log V) (with adjacency lists + heap).

Example implementation#

import heapq

def prim(graph):
    n = graph.V
    visited = [False] * n
    pq = [(0, 0)]  # (cost, vertex)
    total = 0
    while pq:
        cost, u = heapq.heappop(pq)
        if visited[u]:
            continue
        visited[u] = True
        total += cost
        for v, w in graph.adj[u]:
            if not visited[v]:
                heapq.heappush(pq, (w, v))
    return total

Use MSTs where you need to design minimal-cost networks, perform clustering, or connect points efficiently.

How to remove an edge#

In this problem, you must implement the remove_edge function which takes a source and a destination as arguments. If an edge exists between the two, it should be deleted.

Input: A graph, a source (integer), and a destination (integer)

Output: A BFS traversal of the graph with the edge between the source and the destination removed

First, take a close look at this problem and design a step-by-step algorithm before jumping to the implementation. Try it yourself before checking the solution!

Solution#

This challenge is very similar to the deletion in the linked list, if you are familiar with it.

Our vertices are stored in a linked list. First, we access the source linked list. If the head node of the source linked list holds the key to be deleted, we shift the head one step forward and return the graph.

If the key to be deleted is in the middle of the linked list, we keep track of the previous node and connect the previous node with the next node when the destination encounters.

Connectivity, strongly connected components, and Union-Find data structure#

Union-Find (Disjoint Set Union, DSU)#

• Supports two operations:
  • find(x) → which component x belongs to
  • union(x, y) → merge two components
• Useful for cycle detection, connectivity queries, and supporting Kruskal’s algorithm.
• With path compression and union by rank, both operations are nearly O(α(n)) — practically constant.

Finding connected components / SCC in directed graphs#

• For an undirected graph, run DFS/BFS from unvisited nodes to label all reachable nodes — that gives connected components.

• For directed graphs, use Kosaraju’s algorithm or Tarjan’s algorithm to find strongly connected components (SCCs):

  1. Run DFS on the original graph, filling a stack by finish times.
  2. Reverse all edges.
  3. Pop vertices in stack order, running DFS on the reversed graph to collect SCCs.

These algorithms help you decompose the graph into meaningful subgraphs for further processing or analysis.

More interview questions#

Below are other interview questions that you can try your hand at solving:

Additional common graph problems and tips#

Here are more problems and patterns you can try:

• Cycle detection: In directed graphs, detect positive cycles (especially in Bellman–Ford) or feedback loops.

• Topological sort: Order nodes in a directed acyclic graph (DAG). Useful in scheduling and dependency resolution.

• Transitive closure: For directed graphs, compute reachability between every pair (Floyd–Warshall or repeated DFS).

• Graph coloring / bipartiteness check: Use BFS/DFS + coloring to test if graph is bipartite.

• Network flow algorithms: Edmonds–Karp or Dinic’s algorithms to find max flow.

• A search*: For heuristic-based shortest path (especially in grids or spatial graphs).

Tip on complexity and when to choose which algorithm

• Use BFS/DFS for unweighted graphs or connectivity tasks (O(V + E)).

• Use Dijkstra for non-negative weighted graphs of moderate size.

• Use Bellman–Ford when negative edges may exist, but note the higher cost.

• Use Floyd–Warshall when you need distances between all pairs (but only acceptable for small V).

• Use Kruskal/Prim + Union-Find when designing minimal spanning structures.

• Always check whether graph is sparse or dense, directed or undirected, weighted or unweighted — that often dictates your algorithm choice.

What to learn next#

Congratulations on making it to the end. You should know understand graphs in Python and understand what to prepare for graph-related coding interview questions.

If you’d like to learn more about algorithms in Python, check out Educative’s learning path Ace the Python Coding Interview. In these modules, you’ll brush up on data structures, algorithms, and important syntax by practicing hundreds of real interview questions

By the end, you’ll even be able to confidently answer multithreading and concurrency questions.

Happy learning!

Continue reading about coding interviews and Python#

• 3 Month Coding Interview Preparation Bootcamp
• Python 3.9 Updates: topographical sort and string manipulation
• 50 Python Interview Questions and Answers