Check if Two Binary Trees are Identical
Problem Statement
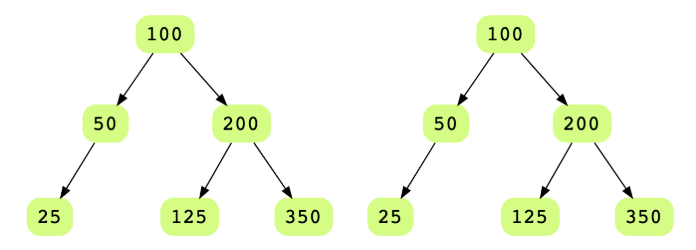
Given the roots of two binary trees, determine if these trees are identical or not. Identical trees have the same layout and data at each node. Consider the following two identical binary trees that have the same layout and data.
It is not necessary that trees that have the same data are identical trees. Trees that have the exact same data may not be structurally identical. For example if you look at the two trees below, although they have the same data, they are not identical.
Hint
- Depth first traversal
- Recursion
Try it yourself
bool are_identical(BinaryTreeNode* root1,BinaryTreeNode* root2) {//TODO: Write - Your - Codereturn false;}
Solution
bool are_identical(BinaryTreeNode* root1,BinaryTreeNode* root2) {if (root1 == nullptr && root2 == nullptr) {return true;}if (root1 != nullptr && root2 != nullptr) {return ((root1->data == root2->data) &&are_identical(root1->left, root2->left) &&are_identical(root1->right, root2->right));}return false;}int main() {BinaryTreeNode *root1 = new BinaryTreeNode(100);insert_bst(root1, 50);insert_bst(root1, 200);insert_bst(root1, 25);insert_bst(root1, 125);insert_bst(root1, 350);display_level_order(root1);BinaryTreeNode *root2 = create_random_BST(15);display_level_order(root2);// Try changing the roots being passedif(are_identical(root1, root2)) {cout<< " the trees are identical" << endl;} else {cout<< "the trees are not identical" << endl;}}
Solution Explanation
Runtime Complexity
Linear, O(n).
Memory Complexity
O(h)
The recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary tree h. It will be O(log n) for a balanced tree and in the worst case can be O(n).
Solution Breakdown
This problem can be effectively solved using a recursive solution. The base case of recursion for this solution is if both nodes being compared are null, or one of them is null.
Two trees ‘A’ and ‘B’ are identical if:
- data on their roots is the same or both roots are null
- left sub-tree of ‘A’ is identical to the left sub-tree of ‘B’
- right sub-tree of ‘A’ is identical to the right sub-tree of ‘B’
To solve this problem, we’ll do a depth-first traversal on both trees simultaneously and keep comparing the data at each level.
Practice problems like this and many more by checking out our Grokking the Coding Interview: Patterns for Coding Questions course!