Linear vs. binary search algorithms

Linear and binary search are two prominent search algorithms. Linear search works well for small sets but fails if the set becomes too large. Binary search works well in most cases, especially when the set is large.

Searching in a small list

Let’s say we have a list of 7 items,

first7Primes = [2, 3, 5, 7, 11, 13, 17]

And we want to check if number 5 is in the list. For this, we would utilize both linear and binary search.

Linear Search

For the linear search, we will go through the list sequentially until we find what we are looking for. It would look similar to this:

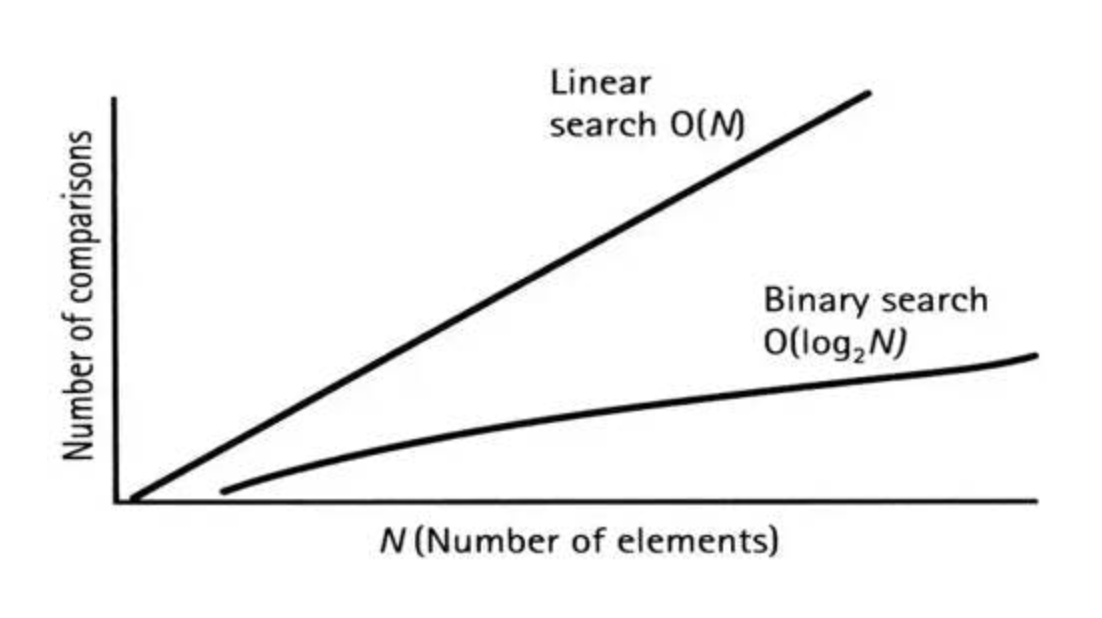
If we are dealing with the first 1000 primes, the time complexity would quickly rise because of the straight-line linear search plot. Below is an image of a straight-line linear search plot vs. that of binary search: Even if you don’t understand BigO notation, you can see that, as the number of search terms increases, the linear search line increases at approximately 45 degrees.

Binary Search

With binary search, we can use the mean of the highest and lowest numbers of the considered set. However, the list has to be ordered for binary-search to work.

How it works

Binary search repeatedly divides the array into halves and computes the average until it lands on the item being searched for. Let’s say we are looking for number 32 in the first 50 whole numbers – we would work through this in pseudocode:

// our set 
first50Numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50]

floor = a function that takes the whole number part of a number

// starting values
minIndex = 0
maxIndex = 49

// iteration 1
roundedAverage = floor((0 + 49)/2) = 24
roundedAverageValue = 25
is 25 < 30? yes, so we ignore anything less than 25. 
minIndex = roundedAverage  + 1 = 25


// iteration 2: minIndex is now 25 instead of 0; maxIndex remains 49
roundedAverage = floor((25 + 49)/2) = 37
roundedAverageValue  = 38
is 38 > 32? yes, so we ignore anything greater than 38. 
maxIndex = roundedAverage  + 1 = 38

// iteration 3: minIndex still remains 25; maxIndex is now 38
roundedAverage = floor((25 + 38)/2) = 31
roundedAverageValue  = 32
is 32 > 32? no, it is equal, so we return True since we've found the number.

The pseudocode is a simplified representation.

Comparing linear and binary

In this array of 50 items, the linear search would perform a maximum of 50 ‘guesses’ while the binary search won’t perform more than 6 (log to base 2 of 50). In the pseudocode above, we only needed 3.

Here’s the code for binary search. We are still using our first array of 7 primes:

from math import floor
first7Primes = [2, 3, 5, 7, 11, 13, 17]
def binarySearch(arr, targetValue):
    array = sorted(arr)
    min = 0
    max = len(array) - 1
    while True:
        average = floor((min + max)/2)
        if (max < min):
            return False
        if (array[average] == targetValue):
            return True
        if (array[average] < targetValue):
            min = average + 1
        else:
            max = average - 1
print(binarySearch(first7Primes, 5)) # True
print(binarySearch(first7Primes, 10)) # False

from timeit import timeit
from math import floor
def linearSearch(arr, item):
    for i in arr:
        if (i == item):
            return True
    return False
def binarySearch(arr, targetValue):
    # array = sorted(arr) to prevent overtime
    array = arr
    min = 0
    max = len(array) - 1
    while True:
        average = floor((min + max) / 2)
        if (max < min):
            return False
        if (array[average] == targetValue):
            return True
        if (array[average] < targetValue):
            min = average + 1
        else:
            max = average - 1
first7Primes = [2, 3, 5, 7, 11, 13, 17]
# First calculation set
print('Small set of numbers')
print(f'Linear takes {timeit(lambda: linearSearch(first7Primes, 5))} seconds')
print(f'Binary takes {timeit(lambda: binarySearch(first7Primes, 5))} seconds')
def largeNumberSet(max):
    numbers = []
    for i in range(max):
        numbers.append(i)
    return numbers
firstOneThousandNumbers = largeNumberSet(1000)
# Second calculation set
print('Large set of numbers')
print(f'Linear takes {timeit(lambda: linearSearch(firstOneThousandNumbers, 422))} seconds')
print(f'Binary takes {timeit(lambda: binarySearch(firstOneThousandNumbers, 422))} seconds')

From the repl above, we see that linear wins over binary when the set is small but loses when the set is large.

Why is any of this important?

The speed of your software depends on the execution speed of your algorithms. To deliver high-quality software, you have to know the right algorithm for the job – you don’t want to keep your users waiting for 10 seconds when the wait time could be less.

Github repo

The code in the repl can be found here.